Omid
Well-known member

Position of the Virtual Image in Binoculars
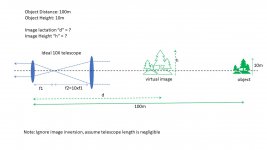
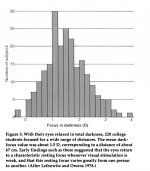
We all know that binoculars are Keplerian telescopes with an inverter (erector) prism added. Consider an ideal afocal telescope as shown in the attached diagram and ignore the erector prisms. Assume that the telescope's magnification power is 10X.
If we point this telescope towards a tree which is 10m tall and located 100m away from an observer's eye. What is the size (h) and location (d) of the virtual image of the tree formed by the telescope?
I look forward to hearing your answers.
-Omid
PS. The above analysis has very significant implications in the way we observer objects through our binoculars. That's why I posed it as a question to motivate the forum members to think about it and discover the answers for themselves. I was shocked when I learned the correct answers for (h) and (d). It wasn't what I was expecting! Upon further investigation, I came across a 1977 paper by Dr. Allan N. Freid (an ophthalmologist from University of California, Berkeley) who provided an accurate account of image location in telescopes. His investigation was triggered by the same "peculiarity" that I was puzzled with: "Why do binoculars or telescopes need precise focusing?" (See Post 131 of this thread).
We all know that binoculars are Keplerian telescopes with an inverter (erector) prism added. Consider an ideal afocal telescope as shown in the attached diagram and ignore the erector prisms. Assume that the telescope's magnification power is 10X.
If we point this telescope towards a tree which is 10m tall and located 100m away from an observer's eye. What is the size (h) and location (d) of the virtual image of the tree formed by the telescope?
I look forward to hearing your answers.
-Omid
PS. The above analysis has very significant implications in the way we observer objects through our binoculars. That's why I posed it as a question to motivate the forum members to think about it and discover the answers for themselves. I was shocked when I learned the correct answers for (h) and (d). It wasn't what I was expecting! Upon further investigation, I came across a 1977 paper by Dr. Allan N. Freid (an ophthalmologist from University of California, Berkeley) who provided an accurate account of image location in telescopes. His investigation was triggered by the same "peculiarity" that I was puzzled with: "Why do binoculars or telescopes need precise focusing?" (See Post 131 of this thread).
Attachments
Last edited: